Compound interest with a R shiny app
Index
This article illustrates the general concept of the compound effect, then the financial implication of the compound interest, and finally a compound interest calculator made with a R web Shiny app.
What is the compound effect
As explained in the book The Compound Effect by Darren Hardy: https://amzn.to/3rymwkj
“The Compound Effect is the principle of reaping huge rewards from a series of small, smart choices over time.”
The exponential benefit of the compound effect is due to the actions accumulated over time…for example if you produce youtube videos the income that you get comes from the new videos that you publish plus all the previous ones.
“Small, Smart Choices + Consistency + Time = RADICAL DIFFERENCE”
In his book Darren Hardy gives examples about how to apply the compound effect to personal development, for example here there a couple of sentences worth to remember:
-
“Preparation (personal growth) + Attitude (belief/mindset) + Opportunity (a good thing coming your way) + Action (doing something about it) = Luck”
-
“If it’s hard, awkward, or tedious, so be it. Just do it. And keep doing it, and the magic of the Compound Effect will reward you handsomely.”
Compound interest
The compound effect can have a huge effect on your personal investments with the compound interest. The huge growth due to the compound interest happens because the investment will create earnings not just from the capital invested but also on accumulated earnings overtime.
For example, for an investment of 100 euro at an interest rate of 10%, the interested generated after one year is 10 euro (=10% of 100 euro), but at the second year the interest will be calculated on the new total capital of 110 euro, so the interest will be 11 euro (=10% of 110 euro) and so on…
| Year | Capital | Interest gained |
|---|---|---|
| 1 | 100 | 10 |
| 2 | 110 | 11 |
| 3 | 121 | 12,1 |
| 4 | 133,1 | 13,31 |
As Warren Buffet said: “My wealth has come from a combination of living in America, some lucky genes, and compound interest”
We can better explain this concept with an example: let’s say that there are two friends, Tom and Jerry, who invest the same total amount of money but along a different time frame.
Tom invests for 20 years 150 euro per month at 5% and an initial investment of 5000 euro, then at the end of the 20 years period he deposited 41.000 euro with a result of 32.418 euro for total interest:
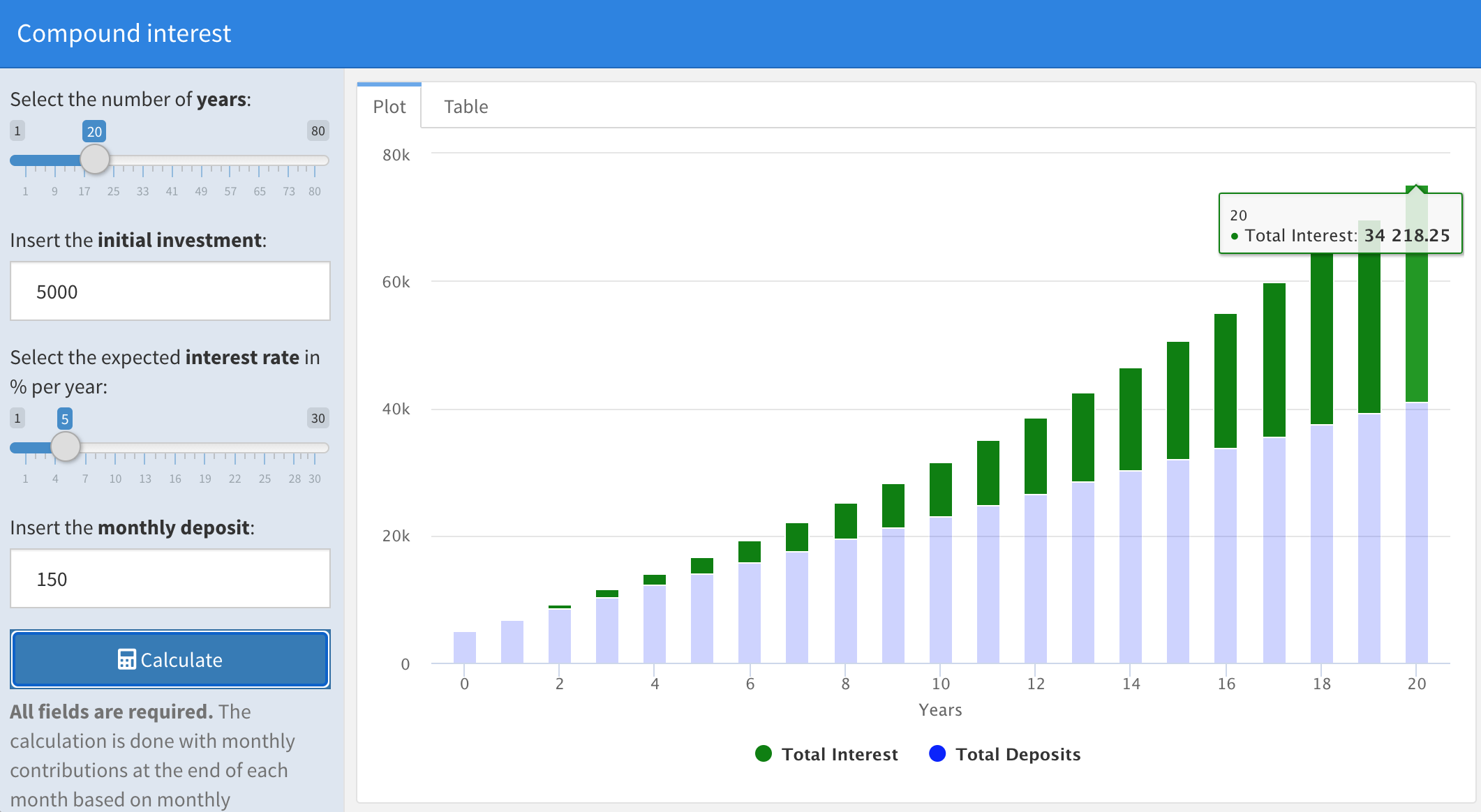
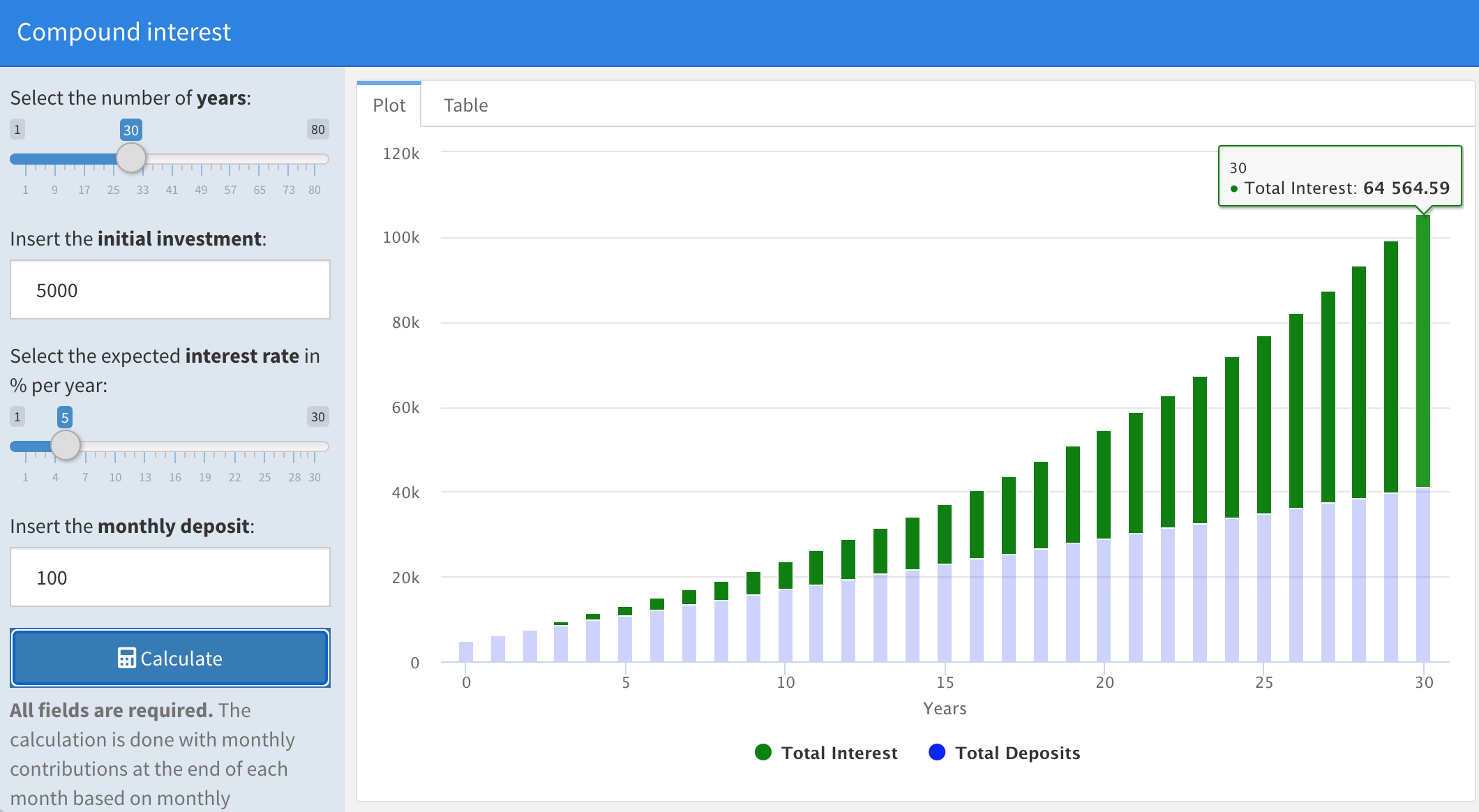
Instead Jerry invests for 30 years 100 euro per month at 5% and an initial investment of 5000 euro, then at the end of the 30 years period he deposited the same total amount of 41.000 euro but with a result of 64.564 euro for total interest:
Therefore, just because of longer time, the same amount of total investments led to much higher interest.
Compound interest formula
This is formula to calculate the compound interest with monthly contributions at the end of each month based on monthly compound intervals.
Total = Compound interest for initial investment + Future value of the monthly deposits
Compound interest for initial investment = $ PV \left(1 + \frac{r}{n}\right)^{(nt)}$
Future value of the monthly deposits = $ MD \cdot \frac {(1+\frac{r}{n})^{(nt)}-1} {r/n} $
so
Total = $ PV \left(1 + \frac{r}{n}\right)^{(nt)}$ + $ MD \cdot \frac {(1+\frac{r}{n})^{(nt)}-1} {r/n} $
where
- Total = total accrued amount of money after t years
- i = interest rate
- PV = present value initial investment
- t = time in years
- n = 12 for the 12 months in a year
- MD = regular monthly deposits
Simple interest
With the simple interest, the interest gained comes only from the initial capital invested and the flow of the interests does not contribute to the total accrued amount.
For example, the table below shows the cash flow of a bond with a fixed interest of 10% per year with an initial capital of 100 euro. The difference with the compound interest is that the cash flow of the interests generated by the bond does not increase the capital at each period.
| Year | Capital | Interest gained |
|---|---|---|
| 1 | 100 | 10 |
| 2 | 100 | 10 |
| 3 | 100 | 10 |
| 4 | 100 | 10 |
Simple interest formula
The variables in the formula for the simple interest are just the initial investment, time and interest rate:
$Total = PV + (PV \cdot i \cdot t) $
where
- Total = total accrued amount of money after t years
- i = interest rate
- PV = present value initial investment
Compound interest calculator with a R shiny web app
At the following link you can simulate different investment scenarios with a compound interest calculator made with a R shiny app:
https://enricotips.shinyapps.io/compound_interest
Code for the compound interest calculator R shiny web app
This is the code for the R shiny app:
---
title: "Compound interest"
output:
flexdashboard::flex_dashboard
runtime: shiny
---
knitr::opts_chunk$set(echo = FALSE)
library(dplyr)
library(tidyr)
library(DT)
library(highcharter)
library(shinyjs)
Inputs {.sidebar}
---------
useShinyjs(rmd = TRUE)
tags$style("#years {width:230px}")
label1 <- HTML(paste0("Select the number of ", strong("years"),":" ))
sliderInput(inputId="years", label =label1, value = 20, min=1, max=80)
# numericInput(inputId="years", label =label1, value = 20, min=0)
tags$style("#PV {width:230px}")
label2 <- HTML(paste0("Insert the ", strong("initial investment"),":" ))
numericInput(inputId="PV", label =label2, value = 5000, min=0)
# sliderInput(inputId="PV", label =label2, value = 5000, min=0, max=1000000)
tags$style("#i {width:230px}")
label3 <- HTML(paste0("Select the expected ", strong("interest rate")," in % per year:" ))
# numericInput(inputId="i", label =label3, value = 5, min=0)
sliderInput(inputId="i", label=label3, value = 5, min=1, max=30)
tags$style("#MD {width:230px}")
label4 <- HTML(paste0("Insert the ", strong("monthly deposit"),":" ))
numericInput(inputId="MD", label =label4, value = 500, min=0)
# sliderInput(inputId="MD", label =label4, value = 500, min=0, max=20000)
tags$style("#Calculate {width:230px}")
actionButton("Calculate", "Calculate", icon("calculator"), style="color: #fff; background-color: #337ab7; border-color: #2e6da4")
helpText(HTML(paste0(strong("All fields are required.")," The calculation is done with monthly contributions at the end of each month based on monthly compound intervals." )))
Column {.tabset}
-------
result <- eventReactive (input$Calculate,{
req(input$years)
req(input$i)
req(input$PV)
req(input$MD)
i <- input$i
i <- i/100
PV <-input$PV
t <- input$years
n <- 12
MD <- input$MD
Balance_vector <- c()
for (y in 1:t){
Balance_partial <- PV*((1+i/n)^(n*y)) + MD *( ( ( (1 + i/n)^(n*y) ) - 1) / (i/n))
Balance_vector <- append(Balance_vector, Balance_partial)
}
Balance_vector <- round(Balance_vector, 2)
Balance_vector <- c(PV, Balance_vector)
Deposit_vector <- rep(n * MD, t)
Deposit_vector <- c(PV, Deposit_vector)
year_vector <- 0:t
compound_df <- cbind(year_vector, Deposit_vector, Balance_vector)
compound_df <- as.data.frame(compound_df)
compound_df$total_deposits <- cumsum(compound_df$Deposit_vector)
compound_df <- compound_df %>% mutate(Total_interest=Balance_vector-total_deposits)
compound_df$Total_interest <- round(compound_df$Total_interest, 2)
compound_df$interest <- compound_df$Total_interest - lag(compound_df$Total_interest)
compound_df$interest <- compound_df$interest %>% replace_na(0)
compound_df$interest <- round(compound_df$interest, 2)
compound_df <- compound_df %>% select(year_vector, Deposit_vector, interest, total_deposits, Total_interest, Balance_vector)
names(compound_df) <- c("Year", "Deposits", "Interest", "Total Deposits", "Total Interest", "Balance")
number_rows <- t+1
list(compound_df=compound_df, number_rows=number_rows)
})
### Plot
highchartOutput("plot")
output$plot <-renderHighchart({
highchart() %>%
hc_chart(type = "column") %>%
hc_xAxis(title = list(text = "Years")) %>%
hc_plotOptions(column = list(
dataLabels = list(enabled = FALSE),
stacking = "normal",
enableMouseTracking = TRUE)
) %>%
hc_series( list(name="Total Interest",data=result()[['compound_df']]$`Total Interest`, color="green"),
list(name="Total Deposits",data=result()[['compound_df']]$`Total Deposits`, color="blue")
)
})
### Table
DT::dataTableOutput("compound_df_table")
output$compound_df_table <-DT::renderDataTable(server = TRUE,(DT::datatable(
result()[['compound_df']], rownames = FALSE,
options = list(scrollY = '450px', pageLength = result()[['number_rows']], dom = 't', ordering=F) ) %>%formatRound(c("Deposits", "Interest", "Total Deposits", "Total Interest", "Balance"), digits = 2) ) )
